- Comme Appelé du Néant — As If Summoned from the Void: The Life of Alexandre Grothendieck (Allyn Jackson) – Part 1 & Part 2
- Alexander Grothendieck: A Country Know Only By Name (Pierre Cartier) Link
-
The Rising Sea: Grothendieck on simplicity and generality I (Colin McLarty) – Link, Video
-
Who Is Alexander Grothendieck? (Winfried Scharlau) Link, Link
Additionally information about Grothendieck can be found at the Grothendieck Circle – – which is where the above image is from.
More to come as I figure out more…
Update #1 (11/13 – 7:18pm): Scott Morrison is also sharing this article over on the Secret Blogging Seminar. Although he includes no exposition, and so I still don’t wanna confirm this.
Update #2: (11/13 – 7:25pm): After a little googling it seems that Liberation is a major daily paper in France circulating over 100,000 papers [Source]. That said a GoogleNews search for “Grothendieck” terms up only one result in the last 24 hours (the Liberation article).
Update #3: (11/13 – 7:41pm): Le Monde is now also reporting on the passing of Alexander Grothendieck. It appears the sad news is most likely true. The above post has been updated to reflect this.
Update #4: (11/13 – 7:57pm): I have been adding additional links to various articles regarding Grothendieck, as well as adding the above picture. A more recent photo of Grothendieck, from the Heidelberg Laureates Forum, can be seen bellow:

Photo from the Heidelberg Laureate Forum
Update #5 (11/13 – 8:08pm): Peter Woit is also blogging about Grothendieck’s passing over on Not Even Wrong. He also points to another blog post for information regarding Grothendieck’s more recent life.
Update #6 (11/14 8:40am): The news has slowly begun to trickle out via english sources, although no major english news providers (NYT, Guardian, the Post, etc.) have ran a story yet. As one might expect many of these stories have focused less on the mathematical resolution that Grothendieck nurtured, but instead on some of the more unusual aspects of his life. That said what hopefully will be a deep, useful, and possibly cathartic discussion of his work has begun over on MathOverflow.
Update #7 (11/14 8:56am): Over on Not Even Wrong Winfried Scharlau, mathematician and author of possibly one of the more complete biographies on Grothendieck, has left the following comment, which is a good reminder for all:
“Grothendieck has passed away, a great man and a great human being. I think it is a matter of respect and a matter of honesty to be very careful with statements about him. The internet is full with wrong, half-true, incomplete, sensational and misleading information about him. Do not believe everyting you read and check everything carefully.
Winfried Scharlau”
Update #8 (11/14 9:23am): The original translations from the Liberation and Le Monde have been edited to reflect the corrections suggested by quasihumanist. Thanks.
Update #9 (11/14 9:29am): The news appears to have finally made its way to english sources, with ABC News and SFGate running the following report from the Associated Press:
“Alexander Grothendieck, an opinionated and reclusive giant of 20th-century mathematics who shunned accolades and supported pacifist and environmental causes, has died, the French presidency said Friday. He was 86.
He died Thursday at hospital in the southwestern town of Saint-Girons, hospital officials said.
Grothendieck was leading mind behind algebraic geometry — a field with practical applications including in satellite communications. He was awarded the Fields Medal in 1966.
According to French daily Le Monde, Grothendieck had been living for years in a hideaway home in the nearby village of Lasserre.
The German-born son of an anarchist Russian-Jewish father and German mother, Grothendieck took his mother’s family name. As World War II neared, he fled to France, and later spent time in an internment camp. His father died in Auschwitz.” — (AP/ABC News)
Hopefully, in the coming days more complete coverage of this will be given.
Update #10 (11/15 – 5:49pm): The larger English media outlets have begun putting out more complete stories on this. In particular, the New York Times has one of the better articles on this I’ve read so far, although it is far from great. Also it included the following line that I find mysterious:
“Mr. Grothendieck’s work was also a steppingstone to solutions of enigmas famous among mathematicians — the Poincaré conjecture, for instance — but far more arcane.”
I did not know that Grothendieck played a part in the proof of the Poincare conjecture. Is this a mistake? If not can someone briefly describe his contribution in this area? The Telegraph also has a very nice obituary, which does a good job not falling into some of the easy cliched narratives that other news agencies have leaned on — i.e lone genius, crazy, etc. Although I feel it does not full delve into the reasons leading to Grothendieck’s break with the mathematical community in the late 1970’s. In different direction a French television station went to the village where Grothendieck apparently spent his last years. Once again my inability to understand French means I have no idea what’s being said. If someone wants to translate this, or has a transcription, I would really thankful. (Thanks to Als over in the comment section of Not Even Wrong for posting this video.)
Update #11 (11/15 – 6:11pm): IHES, the place Grtohendeick spent most of his professional career, has create a webpage in honor of Grothendieck with the following statement:
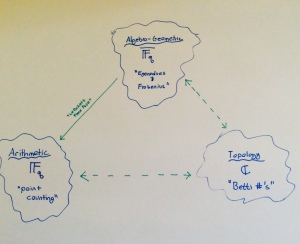
“Grothendieck has profoundly marked the history of mathematics. Hailed as one of the most influential mathematicians of the twentieth century, he considered himself as a ” builder of cathedrals .” Its ambitious fusion arithmetic, algebraic geometry and topology continues to structure contemporary mathematics. IHÉS hosted one of the most extraordinary seminars mathematics, ” Seminar Grothendieck algebraic geometry . The requirement , originality and generosity of spirit Grothendieck founded the Institute . This level of excellence that is brought from a major asset as well as a responsibility for the Institute. The name Alexander Grothendieck is inextricably linked to that of the Institut des Hautes Etudes Scientifiques . IHÉS now wants to make a humble and sincere in this exceptional tribute mathematician.”
Again translated via Google Translate so corrections are appreciated.