(For background on the conference and my time in Utah see my previous updates: Day 1, Day 3, Day 7, Day 14.)
Today marks the 18th and penultimate day of the 2015 AG Institute! This means that yesterday was essentially my last free day in Utah. Having explored the campus and gone hiking I decided to explore downtown Salt Lake more. In particular, I visited Temple Square, which is home to the Mormon Temple, the Tabernacle, and a bunch of museums dedicated to various parts of Mormonism.
Everything was immaculate and beautiful. I was also taken surprised with just how big the temple is. (Apparently this is because I’ve never seen a proper cathedral because some of the conference participants from Europe were surprised with how small it is.) I was also able to go inside the Tabernacle and see a organ recitle. That was somewhat underwhelming, but then again I am not an avid enjoyer of organ music. That said it was pretty cool to at least say I’ve been there. (Pro-tip: Don’t take pictures, even with the flash off, they don’t appreciate that.)
I also spent some time exploring some of the used bookstores downtown. Sadly they didn’t have any interesting math books. (One of them literally had a shelf of random high school algebra solution books that looked to be from the last 15 years. Who in the world goes to a rare book store to buy high school algebra solution books?) That said it was nice to walk around downtown, and I ended up finding a bit of Salt Lake that didn’t feel like one big parking lot!!
Finally, I visited the olympic cauldron from the 2002 Winter Olympics. The cauldron sits next to the University of Utah’s football stadium, and it is a somewhat sad sight. There is no advertisement for it, except one column I had mistake previously mistake for the cauldron.
When you talk towards the torch you eventually find a small room attached to the football ticket office called the Olympic Visitors Center. The room is entirely empty. Even the olympic logo has been removed from the wall. It’s actually kind of sad (especially when one thinks about how much was probably spent on the olympics.)
Finally as always here are a few things I have learned about since last posting:
- Arithmetic, Topology, and Algebra (Jesse Wolfson): Sitting in a French jail cell in 1940, Andre Weil wrote a letter to his sister, Simone Weil, in which he discussed the role of analogy in mathematics. In particular, Weil focused on the growing connections between three fields: algebra, arithmetic, and topology. This letter, which has come to be know has Weil’s Rosetta Stone, has served to inspire a lot of work in mathematics — at least indirectly — over the last 60 years. One nice way to summarize Weil’s analogy is by the following triangle:
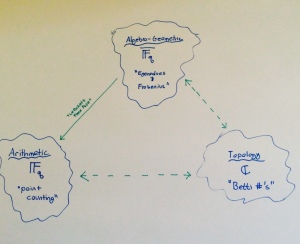Jesse Wolfson gave a very good talk discussing how starting on the topology corner of this triangle one can obtain arithmetic and algebro-gemoeric results. One of the interesting things Jesse Wolfson is doing is that not only is he able to obtain point counts, but he is also able to understand the Galois actions and weights!! I really like when different areas of math connect like this, and I think there is much more to said in this realm. (For example, adding a fourth node to the triangle with motive stuff.) See his papers I & II co-authored with Benson Farb.
- Heuristics For The Rank of An Elliptic Curve (Melanie Matchett Wood): Given an elliptic curve
defined over the rationals the rational points of
where $T$ is the torsion subgroup. Since this was proved in the 1920’s by Mordell people numerous people have work to describe, which groups can appear in this context. For example, in the 1970’s Mazur proved that the torsion subgroup
is one of 15 finite groups! Understanding the rank on the other hand has proven to be more difficult. There have been numerous conjectures — parity principal, boundedness, etc. — but very little unconditional progress on any of theses. Thus, many have spent time creating heuristics for the the rank should behave.Prof. Matchett Wood’s talk focused not on a new heuristic for the rank of elliptic curves (joint work with Jennifer Park, Bjorn Poonen and John Voight.)Since we want to count elliptic curves only up to isomorphism when I say elliptic curve I mean the vanishing set of an equation of the form
where
and if
is a prime such that
then
. Let
be the set of all such elliptic curves. If we are going to do some sort of counting we better be working with finite sets, and so we will partition the set of all elliptic curves by their naive heights. Recall the naive height of an elliptic curve
is equal to the maximum of
and $27 |B|^2$. (Don’t worry about the constants out front.) With all of this in mind we let:
The question the talk tried to answer, or provide a heuristic for answering is: What can be said about:
Note that
is equal to
. I will not go into the specifics of specifics of their model. However, the idea is that consider co-kernels of specific families of random integer matrices, and is motivated by the work of Bhargava et al. on heuristics for the Tate-Schaferavich group. The interesting thing is precisely what their model predicts:
- 50% of elliptic curves have even rank and 50% have odd rank.
- 50% of elliptic curves have rank 0 and 50% have rank 1.
- The Tate-Shaferavich group is finite 100% of the time.
.
- The number of elliptic curves with rank greater than or equal to 21 is finite!!!
PS: Continuing the game of fun things you find in a business school I present you with ethics contests! This raises so many questions: What exactly is an ethics contest? Does the need for an ethics contests suggest a problem with business culture / business school? How would one cheat in an ethics contest?
Fun fact, Spencer Eccles is accused of having helped relatives of IOC members get jobs in the lead up to the bidding process for the 2002 Olympics.
Yellow Pigs 